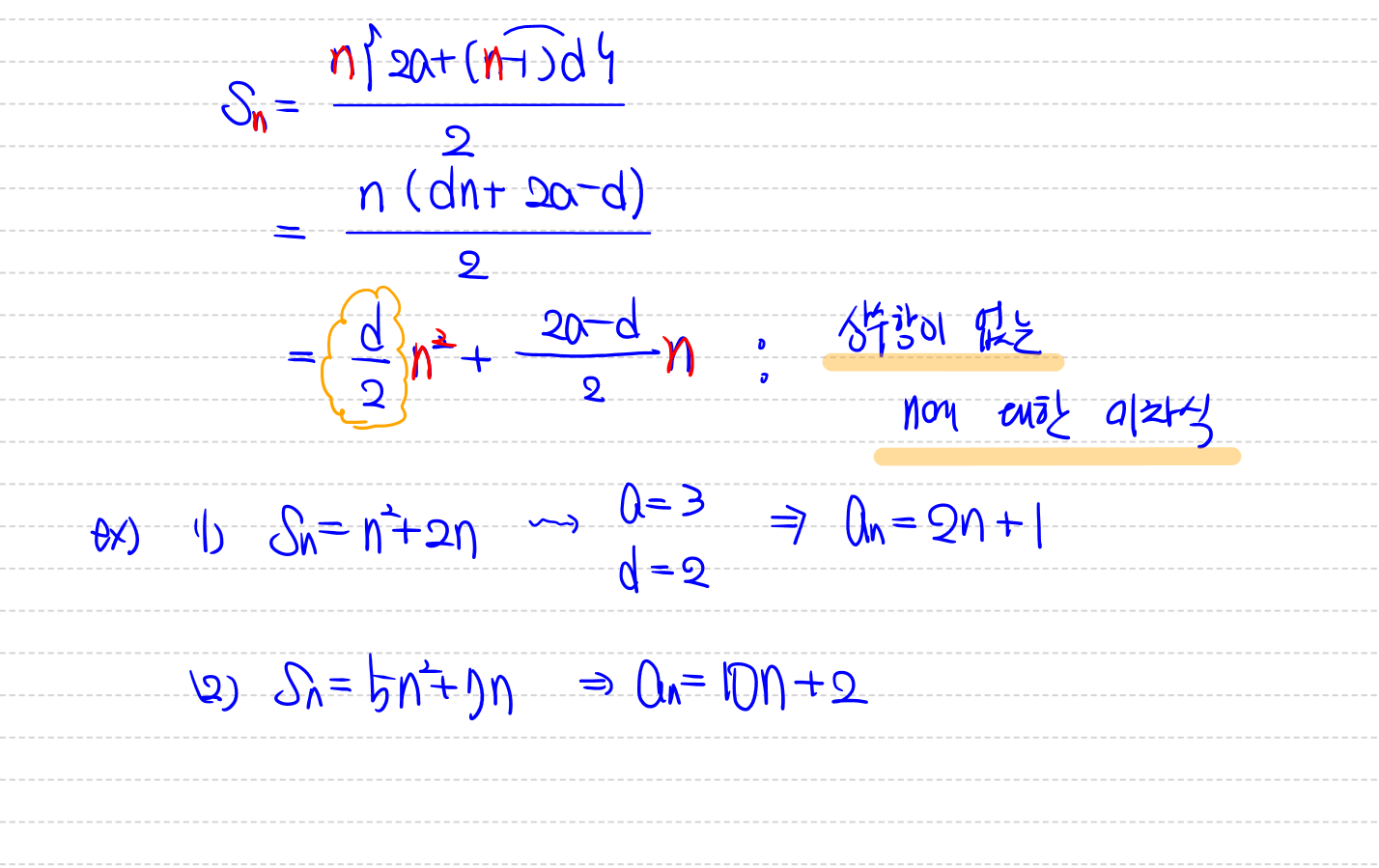
등차수열의 합 공식을 전개해보면 상수항이 없는 n에 대한 이차식임을 알수 있고, 이차항의 계수를 두배한 값이 공차인 것 또한 확인할수 있습니다.
등차수열의 일반항이 n에 대한 일차식이고, 일차항의 계수가 공차라는 구조까지 이해한다면 S_n에서 S_n-1을 뺀 값을 계산하는 과정을 거치지 않고도 등차수열의 합에서 일반항을 바로 구할수 있습니다. 이는 등차수열 전반에 걸쳐 매우 중요하게 다루어지니 반드시 익혀두시기 바랍니다.
'개념정리 및 심화 > 개념정리 및 심화' 카테고리의 다른 글
| 등비수열의 일반항과 합 공식의 구조 분석 (0) | 2021.06.11 |
|---|---|
| 점과 직선사이의 거리의 최댓값 (0) | 2021.06.10 |
| 등차수열의 일반항 구조분석 - n에 대한 일차식으로 해석하여 빠르게 구하기 (0) | 2021.05.28 |
| 거리의 제곱의 합의 최솟값 - 좌표의 평균 (0) | 2021.05.27 |
| 삼차함수의 성질 - 교점에서의 접선의 기울기 (0) | 2021.05.21 |




댓글